The objective of this research is to examine the dissemination of respiratory illnesses, exacerbated by the airborne pollutants emitted by the Figuil cement works, among the local population residing in the vicinity. The primary objective is to examine the impact of pollution, particularly the emission of fine particles and noxious gases, on the transmission of respiratory diseases such as asthma, chronic bronchitis and other lung disorders. The modified SEIR (Susceptible-Exposed-Infected-Recovered) epidemiological model is employed for the analysis of transmission dynamics within the community. This model incorporates environmental, health and demographic variables, thereby enabling the simulation of disease transmission as a function of varying pollution levels. Particular emphasis is placed on vulnerable groups, such as children and the elderly, due to immunosenescence, who are more likely to suffer from the adverse effects of pollution. The results will facilitate the formulation of efficacious strategies, including the implementation of awareness-raising campaigns and the introduction of sophisticated systems for the filtration and capture of pollutants at their source, such as fine particle filters or devices for the reduction of nitrogen oxides (NOx), with the objective of limiting the spread of respiratory diseases in at-risk areas and the formulation of suitable control measures.
| Published in | Mathematical Modelling and Applications (Volume 9, Issue 4) |
| DOI | 10.11648/j.mma.20240904.11 |
| Page(s) | 76-86 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2024. Published by Science Publishing Group |
Air Pollution, Respiratory Diseases, Atmospheric Pollution, Figuil Cement Plant, Fine Particles, Modified SEIR Epidemiological Model
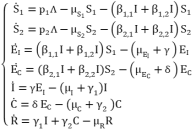 (1)
(1) 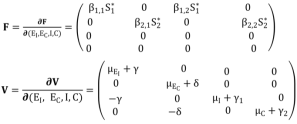

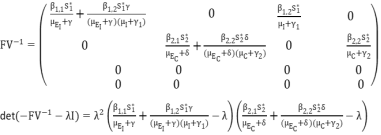
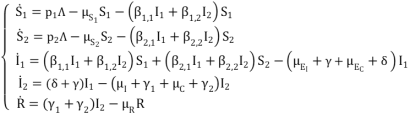 (2)
(2) 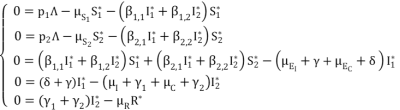 (3)
(3) 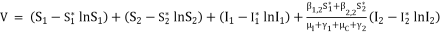
Value (>1) | Value (<1) | Parameters | Value (>1) | Value (<1) | Parameters |
|---|---|---|---|---|---|
0.025 | 0.02 |
| 1 | 1 |
|
0.045 | 0.061 |
| 0.5 | 0.5 |
|
0.076 | 0.05 |
| 0.5 | 0.5 |
|
0.085 | 0.061 |
| 0.01 | 0.01 |
|
0.1 | 0.05 |
| 0.01 | 0.01 |
|
0.1 | 0.05 |
| 0.025 | 0.015 |
|
0.15 | 0.1 |
| 0.043 | 0.085 |
|
0.1 | 0.1 |
| 0.017 | 0.013 |
|
1.0066 | 0.6783 |
| 0.013 | 0.012 |
|
0.1 | 0.1 |
|
NOx | Nitrogen Oxides |
NO2 | Nitrogen Dioxide |
SO₂ | Sulfur Dioxide |
PM2.5 | Particulate Matter with a Diameter of 2.5 Micrometers |
PM10 | Particulate Matter with a Diameter of 10 Micrometers |
SEIR | Susceptible -Exposed-Infected-Recovered |
COPD | Chronic Obstructive Pulmonary Disease |
WHO | World Health Organisation |
DFE | Disease Free Equilibrium |
| [1] | A retrospective study of respiratory diseases in the Figuil area of northern Cameroon. International Journal of Sciences: Basic and Applied Research (IJSBAR) (2023) Volume 67, No 2, pp 38-51. |
| [2] | Y Takeuchi and N. Adachi. The existence of globally stable equilibria of ecosystems of the generalized volterra type. J. Math. Biol., (10): 401–415, 1980. |
| [3] | A Nold. Heterogeneity in disease-transmission modeling. Math. Biosci., 52: 227, 1980. |
| [4] | Jaime Mena-Lorca and Herbert W. Hethcote. Dynamic models of infectious diseases as regulators of population sizes. J. Math. Biol., 30(7): 693–716, 1992. |
| [5] | P. van den Driessche and J. Watmough. reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci., (180): 29–48, 2002. |
| [6] | C. C. McCluskey. Lyapunov functions for tuberculosis models with fast and slow progression. Math. Biosci. Eng., to appear, 2006. |
| [7] | Wei Min Liu, Herbert W. Hethcote, and Simon A. Levin. Dynamical behavior of epidemiological models with nonlinear incidence rates. J. Math. Biol., 25(4): 359–380, 1987. |
| [8] | Michael Y. Li and James S. Muldowney. Global stability for the SEIR model in epidemiology. Math. Biosci., 125(2): 155–164, 1995. |
| [9] | J. A. Jacquez, C. P. Simon, and J. S. Koopman. The repro-duction number in deterministic models of contagious diseases. Comment. Theor. Biol.., 2(3), 1991. |
| [10] | J. A. Jacquez. Modeling with compartments. BioMedware, 1999. |
APA Style
Christophe, K. W., Patrick, N. S., Samuel, B., Jean, N. N., Andre, A. (2024). Investigating Respiratory Disease Transmission Patterns Around the Figuil Cement Works. Mathematical Modelling and Applications, 9(4), 76-86. https://doi.org/10.11648/j.mma.20240904.11
ACS Style
Christophe, K. W.; Patrick, N. S.; Samuel, B.; Jean, N. N.; Andre, A. Investigating Respiratory Disease Transmission Patterns Around the Figuil Cement Works. Math. Model. Appl. 2024, 9(4), 76-86. doi: 10.11648/j.mma.20240904.11
AMA Style
Christophe KW, Patrick NS, Samuel B, Jean NN, Andre A. Investigating Respiratory Disease Transmission Patterns Around the Figuil Cement Works. Math Model Appl. 2024;9(4):76-86. doi: 10.11648/j.mma.20240904.11
@article{10.11648/j.mma.20240904.11,
author = {Kikmo Wilba Christophe and Njionou Sadang Patrick and Batambock Samuel and Nyatte Nyatte Jean and Abanda Andre},
title = {Investigating Respiratory Disease Transmission Patterns Around the Figuil Cement Works
},
journal = {Mathematical Modelling and Applications},
volume = {9},
number = {4},
pages = {76-86},
doi = {10.11648/j.mma.20240904.11},
url = {https://doi.org/10.11648/j.mma.20240904.11},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.mma.20240904.11},
abstract = {The objective of this research is to examine the dissemination of respiratory illnesses, exacerbated by the airborne pollutants emitted by the Figuil cement works, among the local population residing in the vicinity. The primary objective is to examine the impact of pollution, particularly the emission of fine particles and noxious gases, on the transmission of respiratory diseases such as asthma, chronic bronchitis and other lung disorders. The modified SEIR (Susceptible-Exposed-Infected-Recovered) epidemiological model is employed for the analysis of transmission dynamics within the community. This model incorporates environmental, health and demographic variables, thereby enabling the simulation of disease transmission as a function of varying pollution levels. Particular emphasis is placed on vulnerable groups, such as children and the elderly, due to immunosenescence, who are more likely to suffer from the adverse effects of pollution. The results will facilitate the formulation of efficacious strategies, including the implementation of awareness-raising campaigns and the introduction of sophisticated systems for the filtration and capture of pollutants at their source, such as fine particle filters or devices for the reduction of nitrogen oxides (NOx), with the objective of limiting the spread of respiratory diseases in at-risk areas and the formulation of suitable control measures.
},
year = {2024}
}
TY - JOUR T1 - Investigating Respiratory Disease Transmission Patterns Around the Figuil Cement Works AU - Kikmo Wilba Christophe AU - Njionou Sadang Patrick AU - Batambock Samuel AU - Nyatte Nyatte Jean AU - Abanda Andre Y1 - 2024/10/10 PY - 2024 N1 - https://doi.org/10.11648/j.mma.20240904.11 DO - 10.11648/j.mma.20240904.11 T2 - Mathematical Modelling and Applications JF - Mathematical Modelling and Applications JO - Mathematical Modelling and Applications SP - 76 EP - 86 PB - Science Publishing Group SN - 2575-1794 UR - https://doi.org/10.11648/j.mma.20240904.11 AB - The objective of this research is to examine the dissemination of respiratory illnesses, exacerbated by the airborne pollutants emitted by the Figuil cement works, among the local population residing in the vicinity. The primary objective is to examine the impact of pollution, particularly the emission of fine particles and noxious gases, on the transmission of respiratory diseases such as asthma, chronic bronchitis and other lung disorders. The modified SEIR (Susceptible-Exposed-Infected-Recovered) epidemiological model is employed for the analysis of transmission dynamics within the community. This model incorporates environmental, health and demographic variables, thereby enabling the simulation of disease transmission as a function of varying pollution levels. Particular emphasis is placed on vulnerable groups, such as children and the elderly, due to immunosenescence, who are more likely to suffer from the adverse effects of pollution. The results will facilitate the formulation of efficacious strategies, including the implementation of awareness-raising campaigns and the introduction of sophisticated systems for the filtration and capture of pollutants at their source, such as fine particle filters or devices for the reduction of nitrogen oxides (NOx), with the objective of limiting the spread of respiratory diseases in at-risk areas and the formulation of suitable control measures. VL - 9 IS - 4 ER -