The proliferation of panel data studies has been greatly motivated by the availability of data and capacity for modelling the complexity of human behaviour than a single cross-section or time series data and these led to the rise of challenging methodologies for estimating the data set. It is pertinent that, in practice, panel data are bound to exhibit autocorrelation or heteroscedasticity or both. In view of the fact that the presence of heteroscedasticity and autocorrelated errors in panel data models biases the standard errors and leads to less efficient results. This study deemed it fit to search for estimator that can handle the presence of these twin problems when they co- exists in panel data. Therefore, robust inference in the presence of these problems needs to be simultaneously addressed. The Monte-Carlo simulation method was designed to investigate the finite sample properties of five estimation methods: Between Estimator (BE), Feasible Generalized Least Square (FGLS), Maximum Estimator (ME) and Modified Maximum Estimator (MME), including a new Proposed Estimator (PE) in the simulated data infected with heteroscedasticity and autocorrelated errors. The results of the root mean square error and absolute bias criteria, revealed that Proposed Estimator in the presence of these problems is asymptotically more efficient and consistent than other estimators in the class of the estimators in the study. This is experienced in all combinatorial level of autocorrelated errors in remainder error and fixed heteroscedastic individual effects. For this reason, PE has better performance among other estimators.
| Published in | Mathematical Modelling and Applications (Volume 9, Issue 1) |
| DOI | 10.11648/j.mma.20240901.13 |
| Page(s) | 23-31 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2024. Published by Science Publishing Group |
Modified, Method, Panel, Estimator, Simulations
2.1. Model Specification
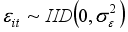 .
. 2.2. Monte-Carlo Experiment
2.3. Data Generating Scheme
 (4)
(4)  The parameters were assigned as.
The parameters were assigned as. 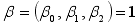
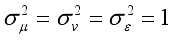
2.4. Derivation of a New Proposed Panel Data Estimator
 binding the regression coefficients vector of
binding the regression coefficients vector of 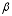 , where R is a row vector of ones defined as
, where R is a row vector of ones defined as N | T=5 | T=10 | |||||
|---|---|---|---|---|---|---|---|
β0 | β1 | β2 | β0 | β1 | β2 | ||
25 | BE | 0.00436 | 0.13246 | 0.11342 | 0.17371 | 0.03544 | 0.22084 |
FGLS | 0.04683 | 0.22915 | 0.61354 | 0.11077 | 0.77631 | 0.01124 | |
ME | 0.00437 | 0.13246 | 0.11343 | 0.17371 | 0.03544 | 0.22084 | |
MME | 0.06349 | 0.0681 | 0.24825 | 0.0499 | 0.03942 | 0.22238 | |
PE | 0.00021 | 0.00031 | 0.00078 | 0.00399 | 0.00011 | 0.00356 | |
100 | BE | 3.72E-06 | 3.82E-08 | 0.03066 | 0.00037 | 0.00011 | 0.01132 |
FGLS | 0.00075 | 0.00662 | 0.04158 | 0.0002 | 0.00785 | 0.05017 | |
ME | 3.70E-06 | 0.00394 | 0.03066 | 0.00037 | 0.00011 | 0.01132 | |
Ugkl; | MME | 0.01193 | 0.00961 | 0.05442 | 0.00866 | 0.00712 | 0.03283 |
PE | 5.29E-06 | 0.00019 | 0.00047 | 0.000017 | 1.02E-04 | 0.00039 | |
200 | BE | 0.00018 | 5.37E-05 | 0.00566 | 0.00031 | 0.00244 | 0.00098 |
FGLS | 0.0001 | 0.00393 | 0.02509 | 0.00422 | 0.01802 | 0.00233 | |
ME | 0.00018 | 5.37E-05 | 0.00566 | 0.00031 | 0.00244 | 0.00098 | |
MME | 0.00569 | 0.00457 | 0.02635 | 0.00604 | 0.00592 | 0.02736 | |
PE | 0.000002 | 6.1E-07 | 0.00019 | 5.15E-06 | 0.000042 | 0.000027 |
N | T=5 | T=10 | |||||
|---|---|---|---|---|---|---|---|
β0 | β1 | β2 | β0 | β1 | β2 | ||
25 | BE | 0.0013093 | 0.0397366 | 0.0340263 | 0.0521136 | 0.0106306 | 0.066251 |
FGLS | 0.0140494 | 0.0687456 | 0.1840608 | 0.0332317 | 0.2328942 | 0.003373 | |
ME | 0.0013095 | 0.0397381 | 0.03403 | 0.0521136 | 0.0106306 | 0.066251 | |
MME | 0.0190483 | 0.0204296 | 0.0744744 | 0.0149688 | 0.0118272 | 0.066713 | |
PE | 0.000064 | 0.0000936 | 0.000235 | 0.0119883 | 0.0000358 | 0.001069 | |
100 | BE | 1.11E-06 | 1.14E-08 | 0.0091979 | 0.0001101 | 3.22E-05 | 0.003396 |
FGLS | 0.0002264 | 0.0019866 | 0.012474 | 6.11E-05 | 0.0023553 | 0.015052 | |
ME | 1.11E-06 | 0.0011827 | 0.0091981 | 0.0001101 | 3.22E-05 | 0.003396 | |
MME | 0.0035777 | 0.0028833 | 0.0163271 | 0.0025988 | 0.0021363 | 0.009848 | |
PE | 3.29E-06 | 0.0000084 | 0.0002032 | 5.32E-06 | 3.37E-05 | 0.000117 | |
200 | BE | 5.51E-05 | 1.61E-05 | 0.0016978 | 9.25E-05 | 0.0007306 | 0.000294 |
FGLS | 3.05E-05 | 0.0011776 | 0.007526 | 0.001265 | 0.0054075 | 0.000699 | |
ME | 5.51E-05 | 1.61E-05 | 0.0016978 | 9.25E-05 | 0.0007306 | 0.000294 | |
MME | 0.0017085 | 0.0013696 | 0.007906 | 0.0018133 | 0.0017767 | 0.008208 | |
PE | 2.66E-06 | 1.8E-07 | 0.0000086 | 1.55E-06 | 0.0000028 | 0.000008 |
N | T=5 | T=10 | |||||
|---|---|---|---|---|---|---|---|
β0 | β1 | β2 | β0 | β1 | β2 | ||
25 | BE | 0.0034915 | 0.10596432 | 0.0907368 | 0.1389696 | 0.0283483 | 0.176669 |
FGLS | 0.0374651 | 0.1833216 | 0.4908288 | 0.0886178 | 0.6210512 | 0.008994 | |
ME | 0.0034921 | 0.10596821 | 0.0907466 | 0.1389696 | 0.0283483 | 0.176669 | |
MME | 0.0507954 | 0.05447904 | 0.1985984 | 0.0399168 | 0.0315392 | 0.177901 | |
PE | 0.000234 | 0.00196221 | 0.0001235 | 0.0000068 | 0.0007244 | 0.000015 | |
100 | BE | 2.97E-06 | 3.05E-08 | 0.0245277 | 0.0002937 | 8.59E-05 | 0.009055 |
FGLS | 0.0006037 | 0.0052976 | 0.033264 | 0.0001629 | 0.0062807 | 0.040139 | |
ME | 2.96E-06 | 0.00315392 | 0.0245281 | 0.0002937 | 8.59E-05 | 0.009055 | |
MME | 0.0095406 | 0.00768891 | 0.0435389 | 0.00693 | 0.0056968 | 0.026261 | |
PE | 1.55E-04 | 0.00070211 | 0.0000962 | 0.0000029 | 3.12E-04 | 0.000055 | |
200 | BE | 0.0001468 | 4.29E-05 | 0.0045276 | 0.0002466 | 0.0019482 | 0.000785 |
FGLS | 8.147E-05 | 0.00314034 | 0.0200694 | 0.0033732 | 0.0144199 | 0.001863 | |
ME | 0.0001469 | 4.29E-05 | 0.0045274 | 0.0002466 | 0.0019484 | 0.000785 | |
MME | 0.0045559 | 0.00365226 | 0.0210826 | 0.0048356 | 0.0047378 | 0.021888 | |
PE | 4.9E-07 | 1.56E-04 | 0.00000412 | 3.8E-07 | 0.0000022 | 0.0000004 |
N | T=5 | T=10 | |||||
|---|---|---|---|---|---|---|---|
β0 | β1 | β2 | β0 | β1 | β2 | ||
25 | BE | 0.052136 | 0.287336 | 0.265776 | 0.329084 | 0.148666 | 0.371028 |
FGLS | 0.170912 | 0.378084 | 0.618576 | 0.262836 | 0.6958 | 0.084084 | |
ME | 0.0521752 | 0.2874144 | 0.265972 | 0.329182 | 0.1486856 | 0.371224 | |
MME | 0.235396 | 0.216188 | 0.415912 | 0.178752 | 0.161504 | 0.378672 | |
PE | 0.003269 | 0.003945 | 0.006256 | 0.014119 | 0.002439 | 0.013334 | |
100 | BE | 0.0304388 | 0.308504 | 0.2765364 | 0.0302604 | 0.0163621 | 0.168033 |
FGLS | 0.043708 | 0.129164 | 0.325556 | 0.02254 | 0.139944 | 0.35378 | |
ME | 0.003038 | 0.0003136 | 0.276556 | 0.0302624 | 0.016366 | 0.168031 | |
MME | 0.17248 | 0.15484 | 0.36848 | 0.147 | 0.13328 | 0.28616 | |
PE | 0.0002320 | 0.000061 | 0.013233 | 0.005950 | 0.001557 | 0.008829 | |
200 | BE | 0.0302428 | 0.01636208 | 0.1680308 | 0.0392134 | 0.1102108 | 0.069952 |
FGLS | 0.02254 | 0.139944 | 0.35378 | 0.14504 | 0.29988 | 0.1078 | |
ME | 0.0302624 | 0.016366 | 0.1680308 | 0.0392196 | 0.1102304 | 0.069972 | |
MME | 0.16856 | 0.15092 | 0.3626 | 0.173656 | 0.171892 | 0.36946 | |
PE | 0.000595 | 0.0003038 | 0.008829 | 0.001433 | 0.007553 | 0.00333 |
N | T=5 | T=10 | |||||
|---|---|---|---|---|---|---|---|
β0 | β1 | β2 | β0 | β1 | β2 | ||
25 | BE | 0.0156408 | 0.0862008 | 0.0797328 | 0.0987252 | 0.0445998 | 0.111308 |
FGLS | 0.0512736 | 0.1134252 | 0.1855728 | 0.0788508 | 0.20874 | 0.025225 | |
ME | 0.0156526 | 0.08622432 | 0.0797916 | 0.0987546 | 0.0446057 | 0.111367 | |
MME | 0.0706188 | 0.0648564 | 0.1247736 | 0.0536256 | 0.0484512 | 0.113602 | |
PE | 0.0009807 | 0.0011835 | 0.0068769 | 0.0042359 | 0.0007319 | 0.004000 | |
100 | BE | 0.0091316 | 0.0925512 | 0.0829609 | 0.0090781 | 0.0049086 | 0.05041 |
FGLS | 0.0131124 | 0.0387492 | 0.0976668 | 0.006762 | 0.0419832 | 0.106134 | |
ME | 0.0009114 | 0.00009408 | 0.0829668 | 0.0090787 | 0.0049098 | 0.050409 | |
MME | 0.051744 | 0.046452 | 0.110544 | 0.0441 | 0.039984 | 0.085848 | |
PE | 0.0000696 | 0.00001835 | 0.003970 | 0.001785 | 0.000467 | 0.002648 | |
200 | BE | 0.0090728 | 0.00490862 | 0.0504092 | 0.011764 | 0.0330632 | 0.020986 |
FGLS | 0.006762 | 0.0419832 | 0.106134 | 0.043512 | 0.089964 | 0.03234 | |
ME | 0.0090787 | 0.0049098 | 0.0504092 | 0.0117659 | 0.0330691 | 0.020992 | |
MME | 0.050568 | 0.045276 | 0.10878 | 0.0520968 | 0.0515676 | 0.110838 | |
PE | 0.000038 | 0.000091 | 0.002648 | 0.000430 | 0.0002659 | 0.000999 |
N | T=5 | T=10 | |||||
|---|---|---|---|---|---|---|---|
β0 | β1 | β2 | β0 | β1 | β2 | ||
25 | BE | 0.0417088 | 0.2298688 | 0.2126208 | 0.2632672 | 0.1189328 | 0.296822 |
FGLS | 0.1367296 | 0.3024672 | 0.4948608 | 0.2102688 | 0.55664 | 0.067267 | |
ME | 0.0417402 | 0.22993152 | 0.2127776 | 0.2633456 | 0.1189485 | 0.296979 | |
MME | 0.1883168 | 0.1729504 | 0.3327296 | 0.1430016 | 0.1292032 | 0.302938 | |
PE | 0.0026154 | 0.00315607 | 0.005005 | 0.0112958 | 0.0019518 | 0.010667 | |
100 | BE | 0.024351 | 0.2468032 | 0.2212291 | 0.0242084 | 0.0130897 | 0.134426 |
FGLS | 0.0349664 | 0.1033312 | 0.2604448 | 0.018032 | 0.1119552 | 0.283024 | |
ME | 0.0024304 | 0.00025088 | 0.2212448 | 0.0242099 | 0.0130928 | 0.134425 | |
MME | 0.137984 | 0.123872 | 0.294784 | 0.1176 | 0.106624 | 0.228928 | |
PE | 0.000185 | 0.00004892 | 0.0048714 | 0.0476045 | 0.0012456 | 0.007063 | |
200 | BE | 0.0241942 | 0.01308966 | 0.1344246 | 0.0313707 | 0.0881686 | 0.055962 |
FGLS | 0.018032 | 0.1119552 | 0.283024 | 0.116032 | 0.239904 | 0.08624 | |
ME | 0.0242099 | 0.0130928 | 0.1344246 | 0.0313757 | 0.0881843 | 0.055978 | |
MME | 0.134848 | 0.120736 | 0.29008 | 0.1389248 | 0.1375136 | 0.295568 | |
PE | 0.000076 | 0.0002431 | 0.0020635 | 0.001146 | 0.0060424 | 0.002664 |
| [1] | Ayansola, O. A. and Adejumo, A. O (2020). A Comparison of Some Panel Data Estimation Methods in the Presence of Autocorrelation and Heteroscedasticity, 4th Professional Statisticians Society of Nigeria (PSSN) International Conference, held at the University of Ilorin, Ilorin, Nigeria. |
| [2] | Ayansola, O. A, and Lawal, D. O (2022); Modeling of Some Economic Growth Determinants in ECOWAS Countries; A Panel Data Approach. International Journal of Scientific & Engineering Research, Vol. (3), 377-385. |
| [3] | Baltagi, B. H., B. C. Jung and S. H. Song (2008). Testing for Heteroscedasticity and Serial Correlation in a Random Effects Panel Data Model. Working paper No. 111, Syracuse University, USA. |
| [4] | Baltagi, B. H., (2005). Econometric Analysis of Panel Data, 3rd Edition, John Wiley & Sons, Chichester, England. |
| [5] | Baltagi, B. H., G. Bresson and A. Pirotte, (2006). Joint LM test for Heteroskedasticity in a One-way Error Component Model. Journal of Econometrics 134, 401-417. |
| [6] | Babak Najafi Bousari, Beitollah Akbari Moghadam (2023). Impact of exchange rates and inflation on GDP’s: A data panel approach consistent with data from Iran, Iraq and Turkey. International Journal Nonlinear Anal. Appl. 14 (2023) 1, 147-161. |
| [7] | Calzolari G., and Magazzini L. (2011). Autocorrelation and Masked Heterogeneity in Panel Data Models Estimated by Maximum Llikelihood. Working paper No. 53, University of Verona. |
| [8] | Garba M. K., Oyejola, B. A. and Yahya, W. A. (2013). Investigations of Certain Estimators for Modeling Panel Data under Violations of Some Basic Assumptions. Mathematical Theory and Modeling, 3(10). |
| [9] | Gujarati, D. (2003). Basic Econometrics. 4th ed. New York. McGraw Hill, pp. 638-640. |
| [10] | Holly, A., Gardiol, I (2000). A Score test for Individual Heteroscedasticity in a One-Way Error Components Model. |
| [11] | Hsiao, C. (2003). Analysis of Panel Data. Cambridge University Press. |
| [12] | Jaba, E., Robu, I. B., Istrate, C., Balan, C. B., Roman, M. (2016). The Statistical Assessment of the Value Relevance of Financial Information Reported by Romanian Listed Companies, Romanian Journal of Economic Forecasting, 19(2), pp. 27-42. |
| [13] | Jirata M. T, Chelule J. C. and Odhiambo R. O (2014) Deriving Some Estimators of Panel Data Regression Models With Individual Effects, International Journal of Science and Research, Volume 3 Issue 5. |
| [14] | Kim, M. S. and Sun, Y. (2011). Spatial Heteroskedasticity and Autocorrelation Consistent Estimation of Covariance Matrix, Journal of Econometrics, 160(2): 349-371. |
| [15] | Lazarsfeld, P. F., & Fiske, M. (1938 Hsiao, C (1985) Analysis of Panel Data. |
| [16] | Li, Q. and T. Stengos (1994). Adaptive Estimation in the Panel Data Error Component Model with Heteroscedasticity of Unknown Form, International Economic Review, 35: 981-1000. |
| [17] | Mazodier, P. and A. Trognon,(1978), Heteroskedasticity and Stratification in Error Component Models. Annales de VINSEE 30-31. 451-482. |
| [18] | Magnus, J. R. (1982). Multivariate Error Components Analysis of Linear and Non-linear Regression models by Maximum Likelihood, Journal of Econometrics 19, 239-285. |
| [19] | Olajide J. T. and Olubusoye, O. E. (2014) Estimating Dynamic Panel Data Models with Random Individual Effect: Instrumental Variable and GMM Approach. |
| [20] | Olajide, J. T, Ayansola O. A and Oyenuga, I. F (2017). Estimation of Dynamic panel Data Models with Autocorrelated disturbance term: GMM approach. Paper presented at 1st international conference of Nigeria Statistical Society on Statistical Research and its Applications. |
| [21] | Olofin, S. O., Kouassi, E. and Salisu, A. A (2010). Testing for Heteroscedasticity and Serial Correlation in a Two-way Error Component Model, Ph.D Dissertation Submitted to the Department of Economics, University of Ibadan, Nigeria. |
| [22] | Phemelo (2018). Dynamic Panel Data Analysis of the Impact of Public Sector Investment on Private Sector Investment Growth in Sub-Saharan African. |
| [23] | Roy, N. (2002). Is Adaptive Estimation Useful for Panel Models with Heteroscedasticity in the Individual Specific Error Component? Some Monte Carlo Evidence, Econometric Reviews, 21: 189-203. |
| [24] | Randolph, W. C., (1998). A Transformation for Heteroscedastic Error Components Regression Models, Economics Letters 27: 349-354. |
| [25] | Uthman and Oyenuga (2021). A Monte- Carlo study of Dynamic Panel Data Estimators with Autocorrelated Error Terms. International Journal of Research/P-ISSN: 2348-6848, Volume 08 Issue 02. |
| [26] | Wansbeek, T. J. (1989). An Alternative Heteroscedastic Error Component Model, Econometric Theory 5, 326. |
| [27] | William H. Greene (2010) Econometric Analysis (5th edition). Prentice Hall, New York, USA. |
| [28] | Yves croissant and Giovanni Millo (2008). Panel data Econometrics in R. |
| [29] | Yuliana Susanti, Hasih Pratiwi, Sri, Sulistijowati H. and Twenty Liana (2014). M Estimation, S Estimation and MM Estimation in Robust Regression, International Journal of Pure and Applied Mathematics, Vol. 91, No. 3, pp. 349-360. |
APA Style
Ayansola, O. A., Adejumo, A. O. (2024). On the Performance of Some Estimation Methods in Models with Heteroscedasticity and Autocorrelated Disturbances (A Monte-Carlo Approach). Mathematical Modelling and Applications, 9(1), 23-31. https://doi.org/10.11648/j.mma.20240901.13
ACS Style
Ayansola, O. A.; Adejumo, A. O. On the Performance of Some Estimation Methods in Models with Heteroscedasticity and Autocorrelated Disturbances (A Monte-Carlo Approach). Math. Model. Appl. 2024, 9(1), 23-31. doi: 10.11648/j.mma.20240901.13
AMA Style
Ayansola OA, Adejumo AO. On the Performance of Some Estimation Methods in Models with Heteroscedasticity and Autocorrelated Disturbances (A Monte-Carlo Approach). Math Model Appl. 2024;9(1):23-31. doi: 10.11648/j.mma.20240901.13
@article{10.11648/j.mma.20240901.13,
author = {Olufemi Aderemi Ayansola and Adebowale Olusola Adejumo},
title = {On the Performance of Some Estimation Methods in Models with Heteroscedasticity and Autocorrelated Disturbances (A Monte-Carlo Approach)},
journal = {Mathematical Modelling and Applications},
volume = {9},
number = {1},
pages = {23-31},
doi = {10.11648/j.mma.20240901.13},
url = {https://doi.org/10.11648/j.mma.20240901.13},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.mma.20240901.13},
abstract = {The proliferation of panel data studies has been greatly motivated by the availability of data and capacity for modelling the complexity of human behaviour than a single cross-section or time series data and these led to the rise of challenging methodologies for estimating the data set. It is pertinent that, in practice, panel data are bound to exhibit autocorrelation or heteroscedasticity or both. In view of the fact that the presence of heteroscedasticity and autocorrelated errors in panel data models biases the standard errors and leads to less efficient results. This study deemed it fit to search for estimator that can handle the presence of these twin problems when they co- exists in panel data. Therefore, robust inference in the presence of these problems needs to be simultaneously addressed. The Monte-Carlo simulation method was designed to investigate the finite sample properties of five estimation methods: Between Estimator (BE), Feasible Generalized Least Square (FGLS), Maximum Estimator (ME) and Modified Maximum Estimator (MME), including a new Proposed Estimator (PE) in the simulated data infected with heteroscedasticity and autocorrelated errors. The results of the root mean square error and absolute bias criteria, revealed that Proposed Estimator in the presence of these problems is asymptotically more efficient and consistent than other estimators in the class of the estimators in the study. This is experienced in all combinatorial level of autocorrelated errors in remainder error and fixed heteroscedastic individual effects. For this reason, PE has better performance among other estimators.},
year = {2024}
}
TY - JOUR T1 - On the Performance of Some Estimation Methods in Models with Heteroscedasticity and Autocorrelated Disturbances (A Monte-Carlo Approach) AU - Olufemi Aderemi Ayansola AU - Adebowale Olusola Adejumo Y1 - 2024/04/02 PY - 2024 N1 - https://doi.org/10.11648/j.mma.20240901.13 DO - 10.11648/j.mma.20240901.13 T2 - Mathematical Modelling and Applications JF - Mathematical Modelling and Applications JO - Mathematical Modelling and Applications SP - 23 EP - 31 PB - Science Publishing Group SN - 2575-1794 UR - https://doi.org/10.11648/j.mma.20240901.13 AB - The proliferation of panel data studies has been greatly motivated by the availability of data and capacity for modelling the complexity of human behaviour than a single cross-section or time series data and these led to the rise of challenging methodologies for estimating the data set. It is pertinent that, in practice, panel data are bound to exhibit autocorrelation or heteroscedasticity or both. In view of the fact that the presence of heteroscedasticity and autocorrelated errors in panel data models biases the standard errors and leads to less efficient results. This study deemed it fit to search for estimator that can handle the presence of these twin problems when they co- exists in panel data. Therefore, robust inference in the presence of these problems needs to be simultaneously addressed. The Monte-Carlo simulation method was designed to investigate the finite sample properties of five estimation methods: Between Estimator (BE), Feasible Generalized Least Square (FGLS), Maximum Estimator (ME) and Modified Maximum Estimator (MME), including a new Proposed Estimator (PE) in the simulated data infected with heteroscedasticity and autocorrelated errors. The results of the root mean square error and absolute bias criteria, revealed that Proposed Estimator in the presence of these problems is asymptotically more efficient and consistent than other estimators in the class of the estimators in the study. This is experienced in all combinatorial level of autocorrelated errors in remainder error and fixed heteroscedastic individual effects. For this reason, PE has better performance among other estimators. VL - 9 IS - 1 ER -